Distinctly
ordered sets are called arrangements or permutations.
Example :
A
flutter on the horses There are 7 horses
in a race.
a) In how many different orders can the horses
finish?
b) How many trifectas (1st , 2nd and 3rd) are
possible?
Solution
:
a) 7.6.5.4.3.2.1=7!
OR 7P7
b) 7.6.5
= 210 or 7P3
Permutations
with Restrictions
In how
many ways can 5 boys and 4 girls be arranged on a bench if there are
a) no
restrictions?
b) boys
and girls alternate?
c) Anne
and Jim wish to stay together?
Solution :
a) 9!
b) A boy
will be on each end BGBGBGBGB = 5.4.4.
3.3.2.2.1.1
Or 5! x
4! or 5P5x4P4
c) (AJ)
_ _ _ _ _ _ _ = 2.8! or 2.8P8
Arrangements
with Repetitions
How many
different arrangements of the word
PARRAMATTA are possible? Arrangements with Repetitions
P A R R
A M
A
TT
A
Solution
: 10 letters but note repetition (4 A’s, 2 R’s, 2 T’s)
No. of
arrangements = 10!/(4! 2! 2! ) = 37 800
Combination
The
number of different combinations (i.e. unordered sets)
No.of
combination = (number of permutations
)/( arrangements of r objects)
Example
:
How many
ways can a basketball team of 5 players be chosen from 8 players?
Solution
:
8C5
Example
2 :
A
committee of 5 people is to be chosen from a group of 6 men and 4 women. How
many committees are possible if
- there are no restrictions?
- one particular person must be chosen on the committee?
- one particular woman must be excluded from the committee?
Solution
:
- 10C5
- 1.9C4
- 9C5
Example
3:
In
a hand of poker, 5 cards are dealt from a regular pack of 52 cards.
In
how many of these hands are there:
All
hearts?
Solution
: 13C5
All the same colour?
Solution:
RED and BLACK
26C5
+ 26C5 = 2.26C5
PERMUTATION & COMBINATION
PROBABILITY
1. As a measure of chance
2. Single events (including listing all the
possible outcomes in a simple chance situation to calculate the probability)
3. Simple combined events (including using
possibility diagrams and tree diagrams, where appropriate)
4. Addition and multiplication of probabilities
(mutually exclusive events and independent events)
Note and Practical Example :
Question 1 :
1) A die is rolled, find the probability that an even number is obtained?
Ans/Solution (Q.1)
·
Let us first write the sample space
S of the experiment.
S = {1,2,3,4,5,6}
S = {1,2,3,4,5,6}
We now use
the formula of the Classical probability.
Question 2 :
2) There are 9 red marbles, 1 green marbles and 5
yellow marbles in a bag. Two marbles are drawn at a random from the bag,one
after another without replacement.
Some of the probability are shown below.
FIRST MARBLE
R = 9/15
G = 1/15
Y = 5/15
SECOND MARBLE
RR GR YR
RR = 8/14 GR = 1/14 YR = 5/14
GR GG
GY GR = 9/14 GG = 0 GY = 5/14
RY GY
YY RY = 9/14 GY = 5/14 YY = 4/14
KEY:
R RED MARBLE
Y YELLOW MARBLE
(a) Calculate
both marble are red,
(c) The two
marbles are of different Color
Ans/Solution (Q.2) :
(a) (9/15 *
8/14) = 12/35
(b) (9/15 *
1/14) + (1/15 * 9/14) = 6/35
(c) (9 /15 * 1/14) + (9/15 * 5/14) +(1/15 * 9/14) + (1/15 * 5/14) +(5/15*9/14) + (5/15 *1/14)
= 59/105
PROBABILITY
Measures of Central
Tendency
The term "measures
of central tendency" refers to finding the mean, median and mode.
Mean- Average
Median- Middle Value,
when the data is arranged in numerical order,
Mode- The value (number)
that appears the most.
Example 1:
Find the mean, median
and mode for the following data:
5, 15, 10, 15, 5, 10,
10, 20, 25, 15.
(You will need to
organize the data.)
5, 5, 10, 10, 10, 15,
15, 15, 20, 25
Example 2 :
On his first 5 biology
tests, Bob received the following scores:
72, 86, 92, 63, and 77. What test
score must Bob earn on his sixth test so that his average (mean score) for all
six tests will be 80? Show how you
arrived at your answer.
Possible solution:
Set up an equation to represent the
situation. Remember to use all 6 test
scores:
72 + 86 + 92 + 63 +
77 + x / 6 = 80
Cross multiply and solve: (80)(6) = 390 + x
480 = 390 + x
- 390 -390 / 90 = x
Bob must get a 90 on
the sixth test.
MEASURE OF CENTRAL TENDENCY
SETS
A collection of "things" (objects
or numbers, etc). Each member is called an element of the set.
Example :
A group of people
{Tall,Fat,Short,Thin,Muscular}
Sets also can be grouped into a Venn diagram.
ԑ = {x : x is a positive integer <14}
A = {x : x divisible by 3}
B = {x
: x divisible by 4}
Draw a Venn diagram to illustrate the
information above.
ԑ = {1,2,3,4,5,6,7,8,9,10,11,12,13}
A = {3,6,9,12}
B =
{4,8,12}
Set Notation :
∈
is an element of
∉
is not an element of
n(A) the number of
elements in set A
n(A’) compliment of set
A
∅
the empty set
ԑ universal set
⊆
is a subset of
⊂
is a proper subset of
∪
union
∩ intersection
Example 2 :
On the venn diagram
below,shade the region representing the sets given.
(a) (A∪B)’
Ans/Solution :
SETS
Introduction
to Statistical Data.
The study of data: how to collect, summarize and
present it.
How
to collect data:
Descriptive (like "high" or
"fast") or Numerical (numbers).
Numerical Data can be Discrete
or Continuous:
Discrete
data is counted,
Continuous data is measured(within a range)
Continuous data is measured(within a range)
Survey:
- Step one: Create
the questions
- Step two: Ask
the questions
- Step three: Tally
the results
- Step four: present the results
How
to Show Data
Pie Charts, the angles formed by each part adds up to
360o
Dot Plots, A graphical display of data using dots.
Line Graphs, a graph that shows information that is connected in some way (such as change over time)
Scatter (x,y) Plots,has points that show the relationship between two sets of data.
Pictographs
Histograms, it is a vertical bar graph with no
gaps between the bars. The area of each bar is proportional to the frequency it
represents.
Frequency Distribution, The organization of raw
data in table form with classes and frequencies.
Stem and Leaf Plots, a diagram that summarises while maintaining the individual data point. The stem is a column of the unique elements of data after removing the last digit. The final digits (leaves) of each column are then placed in a row next to the appropriate column and sorted in numerical order.
Cumulative Tables and Graphs, a plot of the cumulative frequency against the upper class boundary with the points joined by line segments
Question:
1. The table shown no.of kids of technician
in Fade Company.Make a scatter plot by the given data below.
Ans/Solution (Q.1) :
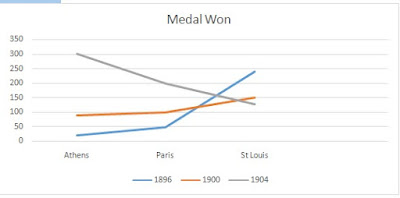
2. Construct a bar graph from the data of medal won
every given years below.
Olympic site
|
1896
|
1900
|
1904
|
Athens
|
20
|
90
|
301
|
Paris
|
47
|
100
|
|
St.Louis
|
239
|
150
|
128
|